-
2. (Matlab) 알아두면 유용한 매트랩, 벡터와 행렬2) Tech 2020. 1. 21. 16:56반응형
안녕하세요! 유용한 기능 두번째 시간이에요!
저번시간에는 matlab으로 Data를 불러와서 원하는 카테고리의 그래프를 그려보고
그래프를 꾸미는 기능에 대해 소개했었습니다.
간단한 그래프를 그리는 법에서 나아가 그래프에 나타난 Data의 특정 열과 행의 계산을 할수도 있습니다.
그러려면 원하는 크기의 행렬을 생성하는 법을 알아야겠죠?
그래서 이번시간에는 벡터와 행렬의 입력에 대해 다뤄보겠습니다!
벡터의 개념을 모르시는 분은 없을 것 같습니다.
그래도 잠깐 짚고 넘어갈게요!
벡터?
- 방향과 크기의 의미를 모두 포함하는 물리적 양(출처: 위키백과)
1. 매트랩에서 벡터의 표현
매트랩에서 벡터는 [] 안에 숫자를 나열하여 표현 됩니다. 아래와 같이요!
- 행벡터
v1 = [1, 2, 3]
v2 = [1 2 3]숫자들을 ,(comma)와 space로 구분하여 나열하여 입력하면 행벡터가 생성됩니다!

행벡터 생성 - 열벡터
v3 = [1; 2; 3]
행벡터와 다르게 ;(semicolon)으로 숫자를 구분하여 나열하면 열벡터가 생성됩니다!
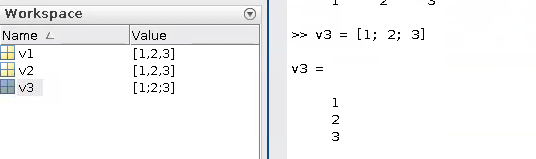
열벡터 생성 저희가 생성한 행벡터는 나열한 숫자의 갯수에 따라 1 x n 행렬이라 볼 수 있겠죠?
그리고 열벡터는 세미콜론으로 추가한 숫자의 갯수에 따라 n x 1 행렬이 됩니다.
그럼 여기서 힌트를 얻어 행벡터와 열벡터를 조합하면 n x m 행렬을 만들수가 있습니다!
- 행렬의 생성
M = [1, 2 ; 3, 4]행렬은 이와 같이 행벡터, 열벡터를 조합하면 생성됩니다!
M = [1,2,3,4; 2,4,4,5; 0,9,3,2;.....]
nxm 은 [a,a1,a2...m; b,b1,b2...m; c,c1,c2...m;...] 으로 표현 되겠죠?!

행렬 생성 그런데 행벡터 생성시 숫자를 일일이 나열해야하는 불편함이 있습니다.
그래서 이를 간편하게 해줄 몇가지 방법이 있습니다!
- linspace 함수 사용
v4 = linspace(0, 100, 101) -> 이를 실행해주면 0 부터 100까지 1씩 증가하는 행벡터가 생성됩니다.
linspace란 함수의 형태는
linspace(a, b, n) 이며
a = 시작점
b = 종료점
n = a~b까지 n등분 하겠다.
를 의미합니다.
즉, v4 = linspace(0, 100, 101)는 0~100까지 101로나누겠다.
0부터 1씩 증가시켜 100까지 도달하는 행벡터를 만들겠다. 라는 의미가 되는거죠!

linspace 함수 사용 예시 그럼 v5 = linspace(0, 100, 11) 는 0~100까지 11등분하겠다. 라는 뜻이 되겠네요!
=> [0, 10, 20, 30, 40 ....100]
- Colon을 이용한 행벡터 생성
위 linspace(0, 100, 101)를 이용해 생성한 행벡터를 콜론 하나만으로 나타낼수 있습니다.
v6 = 0:100 -> 실행하면 동일한 행벡터가 생성됨을 볼 수 있습니다.
v6 = 0:100 는 v6 = 0:1:100 에서 1이 생략된 표기 인데요.!
즉, 0~100까지 1씩 증가시키겠다 라는 의미 입니다.
그럼 이렇게 사용가능합니다!!
v7 = 0:2:9 => 0~9까지 2씩 증가되는 행벡터, 결과: [0, 2, 4, 6, 8]
v8 = 10:-2:1 => 10~-1 까지 -2씩 감소되는 행벡터

colon을 이용한 벡터 생성 콜론과 함수를 이용한다면 벡터 생성을 조금더 간편히 할수 있겠네요!
마지막으로 행렬 Transpose 방법을 알아보겠습니다.
전치 행렬(transposed matrix)은 행과 열을 교환하여 얻는 행렬이다.

전치행렬 예시 (출처: 위키백과- 전치행렬)
매트랩에서 전치행렬 표현은 행렬에 '를 붙여주면 됩니다.즉, A의 전치행렬은 A' 로 표현됩니다.
예시1
A = [1, 2; 3, 4; 5, 6]
Tr1 = A'
입력해볼까요?
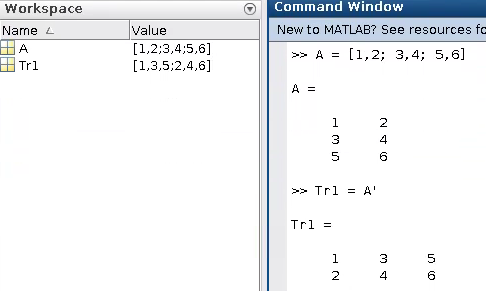
전치 행렬 예시1 잘하셨습니다!!
아래와 같이 선언과 동시에 '를 붙여줘도 적용이됩니다. ㅎㅎ
예시2
Tr2 = linspace(0, 10, 3)';
Tr3 = (1:5)';하지만! 복소수의 Transpose는 아래와 같이 .'를 붙여주어야 Transpose가 제대로 실행됩니다.
c = [1 + 2i, 1-2i]
cTr = c.'그이유는 다음시간에 이야기해보겠습니다!!
오늘은 매트랩의 행렬생성법에 대해 알아봤습니다!
다음시간에는 벡터의 연산으로 찾아 뵙겠습니다.
-------------------------알아두면 유용한 매트랩 2일차 editor----------------------------
%% Vector & Matrix
clear;
clc;
v1 = [1, 2, 3]; % recommend
v2 = [1 2 3];
v3 = [1; 2; 3;];
M = [1, 2 ; 3, 4];
%1~100
vEq = linspace(0, 100, 11);
vEq2 = 0:2:9;
vEq3 = 10:-2:1;
vEq4 = 1:10;
%transpaose
Tr = vEq';
Tr2 = linspace(0, 10, 3)';
Tr3 = (1:5)';
c = [1 + 2i, 1-2i]
cTr = c.'반응형'2) Tech' 카테고리의 다른 글
[Tip!] Jupyter notebook 단축키 모음 (0) 2020.03.02 [Tip!] github에서 csv file(파일) 다운로드 받는 법 (4) 2020.02.28 3. (Matlab) 알아두면 유용한 매트랩, 벡터의 연산 & 통계함수 (2) 2020.02.19 1-2. (Matlab) 알아두면 유용한 매트랩, 다양한 그래프 함수 및 기능 (0) 2020.02.03 1. (Matlab) 알아두면 유용한 매트랩, 그래프 생성 (3) 2020.01.21